T.P. 3 Etude expérimentale des caractéristiques

du Champ magnétique à l'intérieur d'un solénoïde

On appelle solénoïde, un enroulement de conducteur électrique sur un cylindre. Chaque boucle de conducteur est appelée spire.

I. Champ magnétique créé par un solénoïde : direction et sens des lignes de champ :

A l'aide de limaille de fer, on réalise, au bureau le spectre magnétique du solénoïde parcouru par un courant ;

Sur les schémas ci-dessous, dessiner l'aspect des lignes de champ.

Placer des aiguilles aimantées sur pivot afin de repérer le sens du champ. Orienter les lignes de champ dans les deux cas.

vu de côté

vu de côté

 

 

 

  

vu de face

vu de face

 

 

  

Quelle est la propriété des lignes de champ à l'intérieur du solénoïde?

A l'extérieur, le solénoïde se comporte comme un aimant droit; préciser les polarités de cet aimant.

II. Mesures - Présentation du matériel :

Le générateur:

C'est un générateur de courant continu d'intensité réglable (utiliser les bornes rouge et noire les plus à droite). Il est muni d'un ampèremètre numérique intégré.

La bobine:

Sa longueur L = 40,5 cm

Son nombre de spires: N1 = 200 spires entre les deux bornes rouges extrêmes

N2 = 400 spires entre la borne noire d'un côté et la borne rouge de l'autre (les deux autres bornes rouge et noire étant reliées).

branchement pour N = 400 spires

Le teslamètre:

Elle permet de mesurer Bx (selon l'axe de la sonde) ou Bz perpendiculairement à cet axe. Brancher le teslamètre, ne réaliser aucune mesure tant que la lampe en haut à droite est rouge. Sélectionner la commande Bx et le calibre 20 mT

  

III. Manipulations :

- Avant toute connexion mettre les boutons de réglage du générateur sur 0

- Mettre le générateur en marche

- Réaliser le montage ci-contre avec N1 = 200 spires

- Pour le générateur utiliser les bornes rouge et noire les plus à droite

- la sonde étant hors du solénoïde, faire régler le zéro par le professeur.

- La sonde, engagée dans le guide et le repère sur la graduation zéro, est au centre du solénoïde. Vérifier que la valeur de Bx est positive sinon inverser les bornes du générateur

 

1°) Mesurer la valeur de Bx en plusieurs points de l'axe (pour une valeur fixée de I).

2°) a) Placer la sonde au centre. Réaliser environ 8 mesures de Bx pour différentes valeurs de I.

b) Recommencer pour N2 = 400 spires

IV.  Traitement des mesures :

On utilisera le tableur Regressi pour tracer les graphes Bx = f(I)

V. Compte-rendu du TP :

1°) Décrire la première manipulation. Commenter le résultat. Qualifier le champ magnétique à l’intérieur d’un solénoïde.

2°) Imprimer les graphes Bx = f(I). Montrer que les courbes vérifient B = k.I, et déterminer les valeurs de k pour les 2 tracés (soit de façon manuelle soit en utilisant la regression linéaire du logiciel)

Dans le système international d'unités la valeur du champ magnétique B à l’intérieur d’un solénoïde (égale à Bx puisque les lignes de champ sont parallèles à l’axe) a pour expression : B = µ0. NI/L.

Montrer que les résultats obtenus sont compatibles avec cette expression.

Sachant que L = 40,5 cm, évaluer µ0

Sachant que µ0 = 4p.10-7 uSI, déterminer la précision du résultat.

Les Graphes obtenus sur Regressi

(pour ceux qui ne les ont pas imprimés…)

200 spires

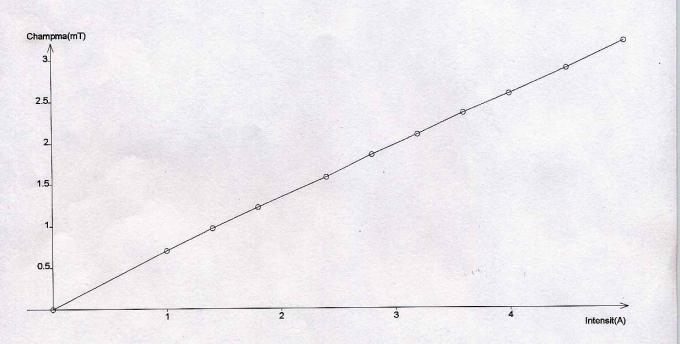
400 spires

Compte rendu du TP

I. Topologie du champ magnétique crée par un solénoïde parcouru par un courant :

1°) Spectre magnétique :

A l'aide de limaille de fer, on a réalisé le spectre magnétique du solénoïde parcouru par un courant ; Les lignes de champ à l'intérieur sont des droites parallèles à l'axe, à l'extérieur, elles sont semblables à celles d'un aimant droit.. Des aiguilles aimantées sur pivot afin de repérer le sens du champ. Leur orientation dépend du sens du courant.

2°) Valeur de B selon l'axe du solénoïde:

Des mesures de la valeur de Bx en plusieurs points de l'axe montrent que Bx reste constant quelle que soit la position à l'intérieur (loin des bords).

3°) Relation entre B et I :

Pour un solénoïde de longueur L = 40,5 cm, et de 200 spires (entre les 2 bornes rouges extrêmes), on mesure B, au centre du solénoïde à l'aide d'un teslamètre:

I (A)

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

B(T)

0

0.32

0.63

0.94

1.29

1.53

1.89

2.15

2.48

2.80

A l'aide d'un tableur, de la calculatrice ou à la main sur du papier millimétré, on trace B = f(I)

Le graphe B=f(I) est une droite passant par l'origine donc B est proportionnel à I.

Le coefficient de proportionnalité k1 peut être obtenu grâce au graphe, en calculant BM/IM pour un point M de la droite.

k1 = 0.62.10-3 T.A-1

Comparons avec la valeur théorique de k(thé) = 4p.10-7xN/L

N = 200 spires; L = 40,5 cm = 0,405 m

k(thé) = 4p.10-7x200/0,405 = 6,2.10-4 uSI

4°) Relation entre B et le rapport N :

Si N est double (à intensité constante) la valeur du champ magnétique au centre est double aussi. (exploitation de la deuxième droite)

B est proportionnelle à N.

II. Conclusions :

A l'intérieur du solénoïde, les lignes de champ sont parallèles et la valeur du champ est constante, le champ magnétique  à l'intérieur d'une bobine parcourue par un courant d'intensité I est donc uniforme.

Dans le système international d'unités, B = 4p.10-7NI/L.