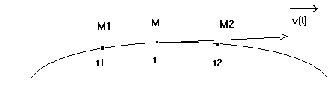Vecteur vitesse - vecteur accélération

I. Objectifs du TP:

Déterminer sur un enregistrement le vecteur accélération du centre d'inertie d'un mobile dans plusieurs cas.

Puis, vérifier la deuxième loi de NEWTON.

II. Rappels de cinématique plane du point matériel :

Soit M un point matériel mobile dans le repère orthonormé fixe (O,) associé au référentiel de la table d'enregistrement

1°) La position de M à chaque l'instant est donnée par: les coordonnées du vecteur sont x(t) et y(t) : = x(t) + y(t) (x(t) et y(t) sont des fonctions du temps) 2°) Le vecteur vitesse de M à chaque instant est représenté par le vecteur: (t) = d/dt de coordonnées: x'(t) = dx(t) /dt et y'(t) = dy(t)/dt (t) = x'(t) + y'(t) (x'(t) et y'(t) sont des fonctions du temps) 3°) Le vecteur accélération de M à chaque instant est représenté par le vecteur: (t) = d/dt = '(t) = d^2/dt^2 = ''(t) de coordonnées: d^2x(t) /dt^2, d^2y(t)/dt^2 ou x''(t), y''(t) (t) = x''(t) + y''(t) (x''(t) et y''(t) sont des fonctions du temps)

III. - Principe des constructions

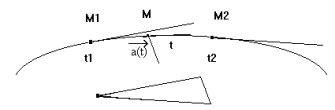
Construction graphique du vecteur vitesse	Construction graphique du vecteur accélération
t) = » M1M2/(t2-t1) L'intervalle de temps (t2-t1) doit être le plus petit possible Le vecteur est toujours tangent à la trajectoire, il est dirigé dans le sens du mouvement.	(t) = » (2 - 1)/ (t2-t1) Le vecteur est dirigé selon2 -1 (vers l'intérieur de la concavité de la trajectoire).

III. Manipulations:

Cas du mouvement circulaire uniforme :

L'enregistrement est obtenu en lançant sur la table à coussin d'air un mobile autoporteur relié à un point fixe par un fil inextensible constamment tendu.

- rechercher le centre du cercle (tracer plusieurs cordes et leurs médiatrices; ces médiatrices sont concourantes en O centre du cercle).

- mesurer son rayon.

- construire (t) en 5 points du cercle (séparés par 2t). Que remarque-t-on pour la valeur de (t)?

- construire (t) aux 4 points intermédiaires du cercle. Que peut-on dire de sa direction? de sa valeur?

- comparer a et v²/R.

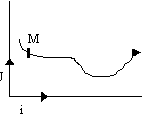
Cas du mouvement d'un solide attaché à un ressort :

L'enregistrement est obtenu en lançant sur la table à coussin d'air un mobile autoporteur relié à un point fixe par un ressort de raideur k supposé sans masse.

- construire (t) en 5 points (séparés par 2t).

- construire(t) aux 4 points intermédiaires.

- à quelles forces le mobile est-il soumis quand le centre d'inertie du solide passe par ces 4 points

- comparer ces 4 sommes des forces aux produits m.a. Conclure.

Cas du mouvement de mercure dans le référentiel héliocentrique (1^er TP) :

Même travail.

Toutes les constructions devront être soignées