TP Déviation d'un faisceau d'électrons en mouvement

dans un champ magnétique uniforme orthogonal à leur vitesse initiale

I. Objectifs du TP :

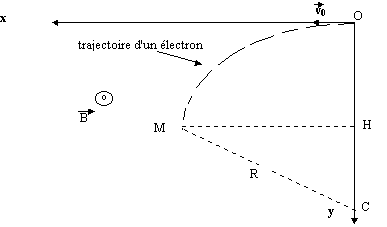
- Vérifier que la trajectoire d'électrons en mouvement dans un champ magnétique uniforme orthogonal à leur vitesse initiale est un arc de cercle.

- déterminer expérimentalement la valeur du rapport e/m.

II. Etude de la trajectoire :

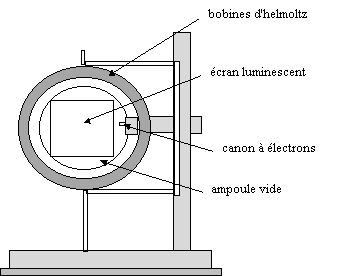1°) Le dispositif expérimental :

Tube Teltron

On choisira :

-  la tension accélératrice du canon à électrons U_AC = 4000 V

-  l'intensité du courant dans les bobines d'helmoltz I_b

telle que y = 2 cm quand x = 10 cm. Noter I_b.

M(x,y) est la position d'un

électron à un instant quelconque

C est le centre du cercle supposé

R est le rayon de courbure

2°) Démarche :

Si la trajectoire est un cercle, on doit vérifier que OC = MC = R

Dans le triangle rectangle MHC, on a MC² = MH² + HC² = MH² + (OC - OH)² soit R² = x² + (R - y)² soit encore après développement et regroupement (à faire) : R =  .

La manipulation consiste donc à relever différentes coordonnées (x,y) de la trajectoire observée, de calculer R à partir de la formule précédemment établie et de vérifier que sa valeur est constante.

3°) Saisie des positions et traitement par un tableur :

- Relever sur l'écran du tube Teltron les coordonnées (x,y) de la trajectoire des électrons pour des valeurs entières de x comprises entre 0 et 10 cm.

- Entrer ces coordonnées dans un tableur (calculatrice, excel, regressi).

- Observer la trajectoire dans un repère orthonormé et vérifier qu'elle correspond à l'observation sur l'écran du tube teltron.

- Calculer pour chaque position (x,y) le rayon de courbure R de la trajectoire.

- Calculer la valeur moyenne de R et  conclure.

- Modéliser la trajectoire y = R - ÖR² -x² en prenant pour R la valeur moyenne calculée.

III. Détermination de la charge massique de l'électron :

1°) Expression et valeur numérique du champ magnétique :

Entre les bobines d'Helmoltz la valeur du champ magnétique (en Tesla) est B =

r est le rayon moyen d'une spire      n est le nombre de spires   I_b est l'intensité du courant dans les bobines

r = 6,8 cm = 6,8.10^-2 m                                         n = 320 spires                                      I_b =

Calculer la valeur de B en Tesla : B =

2°) Application du théorème de l'énergie cinétique dans le canon à électrons:

Etablir l'expression de la vitesse v₀ de l'électron à l'anode de l'accélérateur en fonction de sa charge e, de sa masse m et de la tension accélératrice U_AC.

3°) Application du théorème du centre d'inertie à l'électrons :

Etablir l'expression du rapport e/m en fonction de la vitesse v₀ de l'électron, du rayon R de la trajectoire et de la valeur B du champ magnétique uniforme entre les bobines d'Helmoltz.

4°) Expression de la charge massique de l'électron :

En déduire e/m en fonction de R, B et U_AC

Calculer la valeur expérimentale de e/m.

Comparer à la valeur approchée à partir des valeurs bibliographiques : e = 1,6.10^-19 C et m = 9,1.10^-31 kg

Déterminer l'incertitude relative.