TP Mise en évidence et propriétés de l'auto-induction

I. Rappels de cours :

Le phénomène d'auto-induction est le phénomène d'induction lié à la variation du champ magnétique propre d'une bobine. Une force électromotrice d'auto-induction prend naissance dans un circuit parcouru par un courant d'intensité variable.

Cette f.e.m s'oppose à la variation de l'intensité du courant qui parcourt la bobine : e =

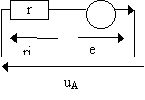
La tension aux bornes d'une bobine soumise à un courant d'intensité variable est u_AB = ri - e = ri +

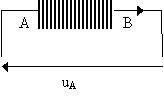
Avec la convention récepteur : équivalent à

II. Objectifs de ce TP :

- réaliser des expériences quantitatives mettant en oeuvre le phénomène d'auto-induction dans un solénoïde.

- acquérir de l'autonomie avec les montages électriques et la manipulation de l'oscillographe.

- rédiger un compte-rendu prédéfini pour préparer l'épreuve expérimentale du baccalauréat.

III. Mise en évidence de l'influence des paramètres du circuit :

Réglages préliminaires de l'oscillographe: Avant de connecter l'oscillographe au circuit, effectuer les réglages qui s'imposent : - intensité et focalisation du spot, - sélection du mode balayage, - visualisation de 2 voies simultanément, - ajustement à zéro des voies - vérification du calibrage des sensibilités, Réglage du GBF: Choisir un signal en créneaux d'une fréquence de 9O Hz. Agir sur le bouton sortie pour obtenir une tension crête à crête de 1V. Jouer sur le décalage du GBF pour observer une tension variable entre 0 et 1V. (oscillographe en mode DC obligatoire pour observer le décalage).

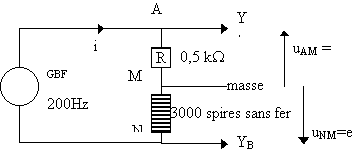
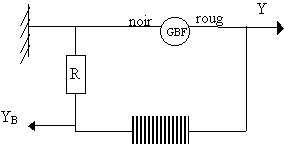
Le circuit à réaliser est le suivant: R réglable de 0 à 1100 W Bobine à 2400 spires.

Appeler le professeur pour vérification

Questions:

Quelles tensions visualise-t-on sur les voies Y_A et Y_B ?

Comparer leurs périodes. Calculer leurs fréquences en précisant la méthode.

Introduire le noyau de fer doux dans la bobine. Quel est son effet sur l’inductance de la bobine ?

Faire le schéma de oscillogramme observé (avec fer doux et R = 500 W).

Diminuer R. Qu'observe-t-on?

Enlever le fer doux et noter les observations. Quelle est l'influence du fer doux ?

Montrer que le quotient L/R est homogène à un temps.

Conclure sur les effets de la variation de R ou de L sur la constante de temps.

IV. Application à la mesure de l'inductance d'une bobine :

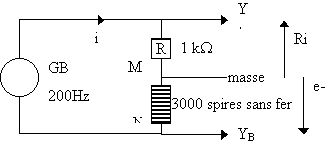
Réaliser le circuit suivant : YA visualise la tension aux bornes de R soit (uAM = Ri) YB visualise NM, l'opposé de la tension aux bornes de la bobine soit e - ri » e (car ri négligeable devant e)

Le GBF délivre maintenant une tension triangulaire. On considère que r <<R (on négligera r devant R) Modifier les réglages du GBF pour que la tension observée en YA varie de -2V à +2V. Questions: 1°) Faire le schéma des oscillogrammes observés. (indiquer les sensibilités et la vitesse de balayage) 2°) Exprimer uNM en fonction de L, R et uAM 3°) Déduire des oscillogrammes la valeur de L

NOM :

Prénom :

Compte rendu de TP (à rendre à la fin de la séance)

I. Mise en évidence de l'influence des paramètres du circuit sur le comportement d'une bobine

Sur la voie Y_A on observe :

Sur la voie Y_B on observe :

Sensibilités choisies : S_H = ; S_V(YA) = ; S_V(YB) =

Période de la tension en Y_A (détailler le calcul) :

Période de la tension en Y_B :

Fréquences :

Commentaire :

Schéma de l’oscillogramme observé (avec noyau de fer doux dans la bobine et R = 500 W) :

Observations : Si R diminue : Si R augmente : Lorsqu'on retire le fer doux : Conclusion sur l'influence du fer doux :

Montrer que le quotient t = L/R est homogène à un temps :

Vérifier la compatibilité des observations avec les effets des variations de R ou de L sur la constante de temps.

II. Application à la mesure de l'inductance d'une bobine :

Schéma de l’oscillogramme observé

Sensibilités choisies : SH = SV(YA) = SV(YB) =

Expression de u_NM en fonction de L, R et u_AM , puis calcul de la valeur de L :

Eléments de correction du TP:

I. Mise en évidence de l'influence des paramètres du circuit sur le comportement d'une bobine:

En voie A : observation de u_GBF = f(t)

En voie B : observation de u_R = Ri = g(t)

même fréquence, celle du GBF.

Lecture de la période sur l’axe horizontal de l’oscillogramme T sur 5 divisions ; Sx = 2ms/div

T » 10 ms ; F = 1/T » 100 Hz (F_réel = 90 Hz)

- si l'on augmente R, l'établissement du courant (régime permanent) est plus rapide.

- si l'on augmente L (noyau de fer doux), l'établissement du courant (régime permanent) est plus lent.

(Remarque u_(GBF) est parfois très déformée par l'influence de la bobine )

Soit L l'inductance totale du circuit et R' sa résistance totale R' = R + r

Montrons que le rapport L/R' est homogène à un temps :

L º V/A/s º V.s/A

R' º V/A

L/R' º s

On dit que t = L/R' est la constante de temps du circuit inductif (comme RC pour un circuit capacitif)

t représente la durée au bout de laquelle i atteint 63% de sa valeur limite à l'établissement du courant ou 37% de sa valeur après la coupure.

Au bout de 5 t le régime permanent peut être considéré comme atteint (à 99%).

II. Application à la mesure de l'inductance d'une bobine :

Réaliser le circuit permettant de montrer que e est proportionnelle à di/dt :

YA visualise la tension aux bornes de R soit i YB visualise NM, l'opposé de la tension aux bornes de la bobine soit e (car r négligeable).

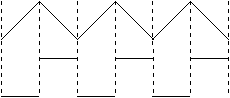
Le GBF délivre une tension triangulaire ; L’intensité i est une fonction linéaire du temps tantôt croissante, tantôt décroissante. Ri est visualisée en YA Comme r ~ 0 , YB visualise e Si i ä; Ldi/dt >0 donc e < 0 (et inversement) i est une fonction linéaire (i = kt), e = -L. di/dt une fonction constante (k)

f = 200 Hz donc T = 5 ms

Sur la première ½ période : u_AM = kt avec k = 4/(2.5.10^-3) = 1600 V/s

u_NM = -0,5 V (valeur constante)

u_AM = Ri ; i = (1/R).(du_AM/dt)

u_NM = e = -Ldi/dt = -(L/R). (du_AM/dt) = -Lk/R

D'où en remplaçant par les valeurs numériques relatives à la première ½ période : L =R/k = 0,15 H