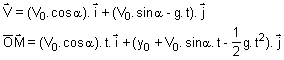NOM :

Prénom :

Contrôle de sciences physiques

Physique I : Détermination approximative de la profondeur du cratère d'un volcan

Deux étudiants, Eric et Aurélie, qui ont un peu oublié la physique qu'ils ont étudiée au lycée, sont au sommet d'un volcan plus ou moins endormi. Son cratère est une sorte de puits dont le fond est toujours sec car les flancs de montagne présentent de nombreuses failles. A quelques mètres du bord du gouffre, ils engagent le dialogue suivant :

A - Aurélie : C'est impressionnant, je me demande si c'est profond.

B - Eric : C'est facile, regarde. Je lance un caillou dans le trou. Attends ! On va entendre le "toc" qu'il fait en arrivant au fond. Un, deux, trois, quatre, cinq, six. Comme z = ½ g.t². Six secondes, ça fait cinq fois trente-six : cent quatre vingt mètres. Le trou fait 180 mètres de profondeur.

C - Aurélie : je doute de la validité de ton truc. Parce que si tu avais pris un caillou plus lourd, son poids aurait été plus important, il aurait donc été attiré plus fort vers le bas et donc il serait descendu plus vite! Et puis ça doit aussi dépendre de la manière de le lancer...

D - Eric : Tu crois, il me semblait pourtant que la formule z = ½ g.t² marchait tout le temps.

E - Aurélie : Et puis, il y a l'air qui freine le caillou.

F - Eric : Bof, en terminale on le négligeait toujours, ça je m'en souviens.

G - Aurélie : Oui, tu as raison, je m'en souviens aussi. Mais, il y a le son : il faut du temps pour qu'il remonte du fond du trou.

H - Eric : D'accord, mais il va vite : 340 m/s. Pour parcourir 180 m, il lui faut grosso modo une demi seconde. Devant 6 secondes, on peut négliger.

I - Aurélie : Tu négliges tout ! tu crois que ton raisonnement tient la route !

J - Eric : Admettons, on tient compte du temps que met le son pour remonter. Le caillou a mis un peu moins de 6 secondes (disons 5,5), il a parcouru ... attends, 5,5 au carré, fois 5 environ 150 mètres. Mais intuitivement, je dirais que cette valeur est une approximation par défaut. A la louche, le puits doit faire entre 160 et 170 mètres de profondeur.

K - Aurélie : Bingo ! Regarde la pancarte là-bas : "Profondeur 160 mètres". Ah ! j'aurais jamais cru que mes cours de physique de terminale pouvaient encore me servir...

Répondre aux questions suivantes à propos de ce dialogue :

I. 1°) Enoncer le théorème fondamental de la dynamique

2°) L'appliquer pour déterminer l’équation horaire du mouvement sur un axe vertical. Préciser les hypothèses (repère, conditions initiales).

3°) Comment Eric doit-il lancer le caillou pour pouvoir utiliser l'équation horaire z = ½ g.t² ?

II. 1°) Faire la liste des objections apportées par Aurélie au calcul d'Eric. Parmi ses propositions, préciser en justifiant celles qui sont scientifiquement fausses.

2°) Déterminer la relation qui existe entre la profondeur du trou z et le temps T qui s'est écoulé entre le lancer et la perception du "toc" sans négliger le temps que met le son pour remonter du fond. Faire l'application numérique pour z = 160 et z = 180 m. Conclure.

Donnée : g =9,8 N/kg

0,25

1,25

0,5

PHYSIQUE II : Mouvement du centre d'inertie d'une balle

Une balle de masse m = 60 g, lancée à la vitesse avec un angle a par rapport à l'horizontale, est filmée avec un caméscope. Les positions successives de son centre d'inertie, représentées par un point M de coordonnées (x,y) dans le repère orthonormé (O,) où est porté par l'horizontale et dirigé vers la droite et où est porté par la verticale et dirigé vers le haut, sont enregistrées puis les données obtenues subissent un traitement informatique à l'aide d'un logiciel adapté. Ce logiciel permet de tracer les graphiques suivants (documents 1 à 5). Les frottements de l'air sur la balle sont négligeables. A l'instant t = 0, on suppose que M est en M₀ de coordonnées (x₀ = 0,y₀). Quand t = t₁, la balle effectue un rebond sur le sol.

La balle se déplace dans un champ de pesanteur uniforme d'intensité g. L'expression de l'accélération de son centre d'inertie est :

I 1. Montrer que lorsque 0 < t < t₁ les expressions de la vitesse et de la position de M en fonction du temps sont données par :

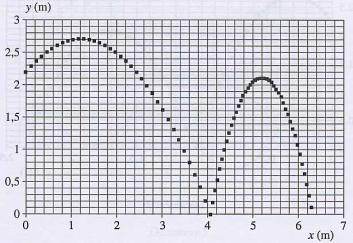
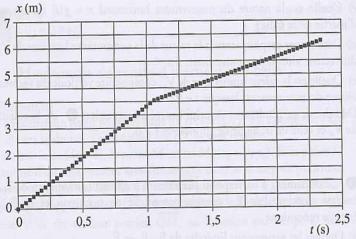
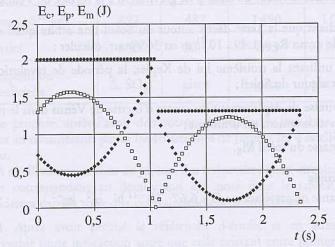
2. Identifier parmi les documents, celui qui représente la trajectoire du centre d'inertie de la balle.

3. Quelle est la valeur de t₁ ?

4. Etablir, à partir des données, l'équation de la trajectoire du centre d'inertie lorsque 0 < t < t₁ ;

vérifier qualitativement sa compatibilité avec l'allure du tracé.

II. 1. Quelle est la nature du mouvement vertical y = f(t) du centre d'inertie de la balle ?

2. Que représente le coefficient directeur des portions de droites parallèles du document 4 ?

En déduire une valeur approchée de g

3. Quelle est la nature du mouvement horizontal x = g(t) du centre d'inertie de la balle ?

4. Déterminer graphiquement la valeur de la composante horizontale V_x du vecteur vitesse si t < t₁.

5. Quelle est la valeur numérique de V_y, composante verticale du vecteur vitesse lorsque t = 0.

6. Déduire de ces deux derniers résultats la valeur de V₀ ainsi que l'angle a (angle de tir quand t = 0)

III. Le document 5 donne l'évolution de l'énergie cinétique Ec, de l'énergie potentielle de pesanteur Ep et de l'énergie mécanique Em en fonction du temps.

1. Donner les expressions littérales de Ec, Ep et Em (on prendra Ep = 0 lorsque y = 0)

2. Identifier sur le document 5 les courbes représentant Ec, Ep et Em en justifiant soigneusement la réponse.

3. Quelle est la particularité présentée par la courbe représentative de Em lorsque t = t₁ ? Proposer une explication.

0,25

0,75

0,25

0,5

0,25

0,5

0,75

0,5

Chimie I : Dosage d'un détartrant pour cafetière

Données : Masses molaires en g.mol^-1 : M(H) = 1 ; M (O ) = 16 ; M(N) = 14 ; M ( S ) = 32 ; M(acide sulfamique) = 97

Zone de virage des indicateurs colorés :

- hélianthine ( 3,1 – 4,5 )

- bleu de bromothymol ( 6 – 7,6 )

- phénolphtaléine ( 8,2 – 10 )

1 . Un détartrant pour cafetière vendu dans le commerce se présenta sous la forme d'une poudre blanche, l'acide sulfamique

H₂N – SO₃H que l'on considère comme un monoacide fort et que l'on notera par la suite AH.
a. Rappeler ce qu'est un acide fort.
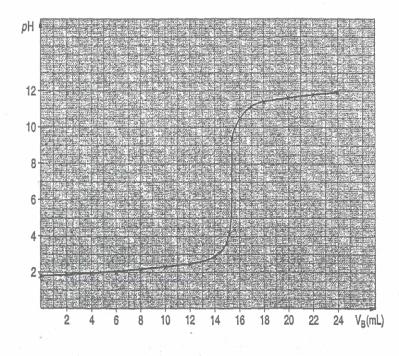
b. Ecrire l'équation-bilan de la réaction avec l'eau de l'acide sulfamique

2. On dissout 1,50 g de ce détartrant dans de l'eau distillée à l'intérieur d'une fiole jaugée de 200mL que l'on complète ensuite au trait de jauge . On procède à son dosage par une solution titrée de soude (solution d'hydroxyde de sodium) de concentration c_B = 0,10 mol.L^-1. Le suivi de ce dosage se fera avec un ph-mètre. Aux 20 mL de solution S, on ajoute 80 mL d'eau afin de pouvoir immerger correctement la sonde pH-métrique. Faire un schéma annoté du dispositif de dosage.

3. On obtient la courbe ci-après document 6.

a. La forme de la courbe obtenue permet-elle de vérifier que l'acide dosé est un acide fort.

b. Ecrire l'équation-bilan de la réaction chimique support du dosage.

c. A partir de la courbe, déterminer les coordonnées du point d'équivalence, en faisant apparaître sur le graphique la méthode utilisée. En déduire la concentration c_A de la solution S.

d. Calculer la masse d'acide sulfamique présente dans S ; en déduire le pourcentage r de substance dans le détartrant étudié.

e. Si le dosage avait été réalisé en présence d'un indicateur coloré, lequel aurait été le plus approprié ? Justifier

f. Un élève en séance de TP trouve r = 102 %. Si l'erreur vient de la pesée l’évaluation de la masse est-elle supérieure ou inférieure à la masse réelle ? Justifier rapidement. Quelles peuvent être les autres sources d'erreur ?

0,25

0,75

0,5

0,25

CHIMIE II : Cinétique chimique.

Pour étudier, à température constante et en milieu acide, la cinétique de la réaction entre l’ion permanganate et l’acide oxalique H₂C₂O₄, on réalise l’expérience suivante :

A la date t = 0, on mélange rapidement, en présence d’un excès d’acide sulfurique, un volume V₁ = 40 mL d’une solution aqueuse (S₁) de permanganate de potassium de concentration C₁ = 5,0 x 10^-3 mol.L^-1 et une volume V₂ = 60 mL d’une solution aqueuse (S₂) d’acide oxalique de concentration C₂ = 5,0 x 10^-2 mol.L^-1.

La couleur d’une solution contenant des ions permanganate dépend fortement de la concentration de ces ions. On utilise cette propriété pour déterminer la concentration [] à chaque instant (dosage colorimétrique).

1. Réaction étudiée

L’équation-bilan de la réaction s’écrit : 2 + 5 H₂C₂O₄+ 6 H₃O⁺ Õ 2 Mn²⁺ + 10 CO₂ + 14 H₂O (1)

Les couples d’oxydo-réduction qui interviennent sont /Mn²⁺ et CO₂ / H₂C₂O₄.

Ecrire les demi-équations d’oxydo-réduction correspondant aux couples précédents.

2. Préparation des solutions

a ) Calculer en moles la quantité n₁ d’ions permanganate présents à t = 0 dans le mélange réactionnel.

b ) Quelle est, en moles la quantité n₂ d’acide oxalique nécessaire pour réduire au bout d’un temps assez long tous les ions permanganate ? En a-t-on suffisamment introduit dans le mélange réactionnel initial ?

3. Expérience

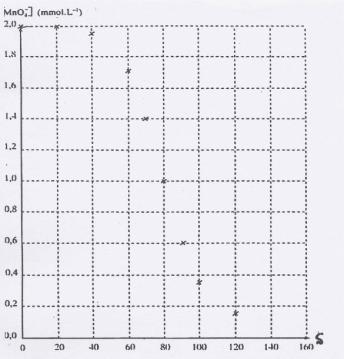
L’étude colorimétrique donne les résultats portés sur la courbe ci-après document 7.

a) Définir la vitesse instantanée de disparition des ions . Déterminer la valeur de cette vitesse à l’instant t = 80 s.

b) Comment varie la vitesse de disparition des ions au cours de l’expérience ?

Une propriété assez générale en cinétique chimique est que la vitesse de disparition des réactifs diminue quand les concentrations de ceux-ci diminuent. Cette propriété vous paraît-elle vérifiée dans l’expérience envisagée ?

Quelle serait l’allure de la courbe si tel était le cas ?