TS2 Contrôle de Sciences Physiques
Physique :
I. Questions de cours :
Définir et préciser les conditions d’observations de la résonance mécanique.
II. Dipôle RC :
On veut étudier en TP la réponse d'un dipôle RC à une tension en créneaux (de valeur minimale 0V et de valeur maximale 2V). On réalise donc un circuit comportant le GBF, un condensateur de 1µF et un conducteur ohmique 103 W.
1°) Faire le schéma du montage en spécifiant les branchements d'un oscilloscope bicourbe permettant de visualiser simultanément l'évolution au cours du temps de la tension uC aux bornes du condensateur et celle de la tension aux bornes du GBF.
2°) Calculer la valeur du produit RC. Que représente physiquement cette grandeur?
3°) Donner une valeur approchée de la durée de la charge du condensateur.
4°) La fréquence du GBF est de 100 Hz. Dessiner très précisément l’observation sur l’écran de l’oscilloscope de la tension aux bornes du générateur. (on suppose que la base de temps est choisie de façon à visualiser au moins une période complète du générateur). On représentera une période du générateur avec l’échelle imposée suivante : 1 division pour 25 ms ; 1 division pour 0,5 V
5°) Superposer à la représentation graphique précédente, celle de l’observation sur l'écran de l'oscilloscope, de la tension aux bornes du condensateur. On fera apparaître sur ce graphique la valeur du produit RC.
6°) On diminue alors la fréquence du GBF décrire l’évolution de l’oscillogramme.
7°) La fréquence du GBF étant remise à 100 Hz, on change la résistance pour une de 10 W (tous les autres paramètres étant identiques). Comment l'oscillogramme est-il modifié?
III. Etude d'un oscillateur élastique vertical :
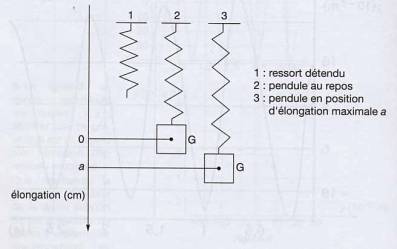
On dispose d’un pendule vertical constitué :
- D’un ressort de masse négligeable et de raideur k
- D’une charge de masse m, de centre d’inertie G.
Ce pendule est un système dont on peut enregistrer l’élongation en fonction du temps à l’aide d’un dispositif relié à un ordinateur. Ce dispositif n’est pas représenté sur le schéma ci-dessous. On note a l’amplitude des oscillations du pendule.
1
1
1.5
1
0.5
1
2
0.5
0.5
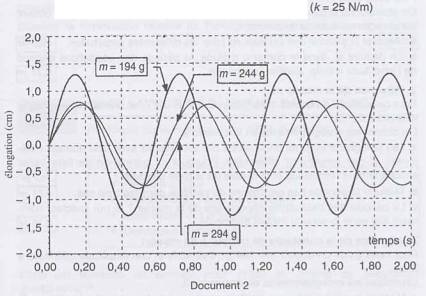
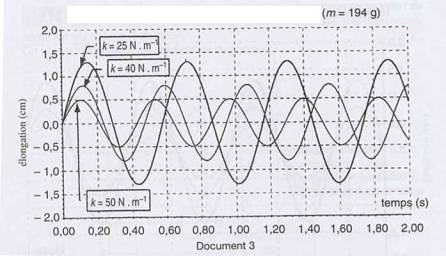
I - On souhaite étudier l'influence des paramètres : masse, constante de raideur du ressort, amplitude initiale, sur la période des oscillations du pendule. Au cours des expériences suivantes, on garde constants tous les paramètres envisagés sauf celui dont on étudie les effets.
Le pendule est écarté verticalement de sa position de repos, on déclenche le système d'enregistrement de l'élongation en fonction du temps puis on abandonne le pendule qui se met à osciller.
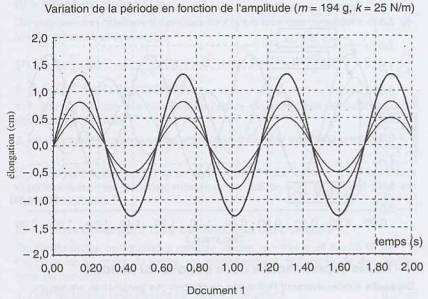
1. En analysant les courbes de variation de l'amplitude du pendule en fonction du temps (documents 1, 2 et 3), préciser et justifier quelles sont les propositions vraies.
• Proposition 1 : l'enregistrement débute au moment où on abandonne le pendule.
• Proposition 2 : l'enregistrement débute au moment où le pendule passe par sa position de repos en montant.
• Proposition 3 : la durée d'enregistrement est égale à deux secondes.
0.75