Modélisation des systèmes oscillants

1°) équations différentielles :

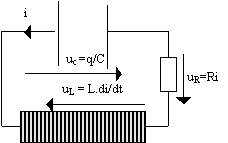
	oscillateur mécanique ressort horizontal (k) - masse (m)	oscillateur électrique dipôle RLC série
schéma	x = position du CDI de la masse sur l'axe horizontal	q = charge du condensateur ; uC = tension à ses bornes (uC = q/C avec la convention récepteur)
méthodes d'étude	1°) Bilan des forces appliquées à la masse - application du théorème du centre d'inertie - projection sur l'axe Ox 2°) sans amortissement : conservation de l'énergie mécanique	1°) Loi des mailles uC + uR + uL = 0 2°) Si R = 0 : conservation de l'énergie électrique
oscillations libres sans amortissement	sans frottement x" + (k/m).x = 0 = x' = x"	R = 0 pas de dissipation d'énergie par effet Joule q" + 1/(LC).q = 0 u" + 1/(LC).u = 0 i = intensité du courant électrique: i = q'
oscillations libres avec amortissement fluide	avec frottement du type: = - µ x" + (µ/m).x' + (k/m).x = 0	R ¹ 0 dissipation d'énergie par effet Joule q" + (R/C).q' + 1/(LC).q = 0 u" + (R/C).u' + 1/(LC).u = 0

2°) solutions :

type de l'équation différentielle	solutions	oscillateur mécanique ressort horizontal (k) - masse (m)	oscillateur électrique dipôle LC série
oscillations libres sans amortissement y" + w0^2y = 0	y = Ymcos(w0t+j)	x = X0cos(w0t+j) w0^2 = k/m X0 et j définis par les conditions initiales	u = U0cos(w0t+j) w0^2 = 1/LC U0 et j définis par les conditions initiales
oscillations libres avec amortissement y" + 2ay' + w0^2y = 0 polynôme associé : r^2 + 2ar + w0^2 = 0 D' = a^2 - w0^2	si a^2 > w0^2; 2 racines réelles pour le binôme associé: y =K1exp-(a+Ö(a^2- w0^2)) t + K2exp-(a-Ö(a^2- w0^2)) t si a^2 = w0^2; 1 racine double pour le binôme associé: y =(a.t+b).exp(-a.t) si a^2 < w0^2; 2 racines complexes conjuguées pour le binôme associé: y =K.[exp-a.t].cos[(Ö(w0^2- a^2)) t + j]	régime apériodique surcritique; retour à l'état d'équilibre sans osciller K1 et K2 dépendent des conditions initiales régime critique, retour rapide à l'état d'équilibre; a et b dépendent des conditions initiales régime pseudo périodique de période w=Ö(w0^2- a^2)@ w0 si a faible K et j dépendent des conditions initiales	régime apériodique surcritique; décharge du condensateur sans osciller K1 et K2 dépendent des conditions initiales régime critique, retour rapide à l'état d'équilibre; a et b dépendent des conditions initiales régime pseudo périodique de période w=Ö(w0^2- a^2)@ w0 si a faible K et j dépendent des conditions initiales

oscillations forcées sans amortissement	Générateur de force d'amplitude F et de pulsation w x" + (k/m)x = Fcos(wt)	Générateur basse fréquences d'amplitude U et de pulsation w u" + 1/(LC)u = Ucos(wt)
oscillations entretenues		équation non linéaire pour rendre compte de la stabilisation des oscillations: q"+ e((q^2/a^2) - 1)q' + 1/(LC)q = 0 (modèle de Van der Pol)