I. La codification de l'information :

Le langage est la faculté d'exprimer et de communiquer sa pensée au moyen de signes. Notre langage écrit utilise un code basé sur 26 lettres (majuscules et minuscules), 10 chiffres, des symboles de ponctuation, des signes mathématiques. Grâce à ce code et à ses règles nous pouvons transmettre des informations,  donner des instructions, dénombrer...

Bien que les ordinateurs soient qualifiés "d'intelligence artificielle", ils n'ont aucune faculté d'appréhender le monde extérieur. Leur seule intelligence réside dans leur rapidité d'exécution de combinaisons d'ordre à deux états.

Le langage des ordinateurs dérive d'un code binaire que l'on peut schématiser par (0 ; 1), (non ; oui), (éteint ; allumé)...

Le pionnier du langage binaire est le britannique Francis Bacon (1561 - 1626 ; homme d'Etat, philosophe, essayiste). Il imagina ce code pour crypter les messages diplomatiques secrets. Chaque lettre de l'alphabet était remplacée par un mot composé de 5 lettres ne contenant que des A et des B.

C'est Gottfried Wilhem von Leibniz (1646 - 1716 ; philosophe et mathématicien allemand) qui contribua directement (mais sans grand succès à son époque) au développement de l'informatique en formalisant les combinaisons de 0 et de 1 qui constituent le code binaire moderne. Ce code à 2 états a trouvé son application avec l'apparition des relais (sortes d'ampoules électriques à 2 états aussi : ouvert ou fermé). Les premiers ordinateurs étaient donc des calculateurs.

Une des premières applications fut aussi l'automatisation de l'industrie textile en 1804 : le français Joseph-Marie Jacquard (1752 - 1834) améliora la technique de commande des métiers à tisser en y associant des cartes perforées transportées par une bobine mobile, un trou correspondant à l'état "ouvert" et l'absence de perforation à l'état "fermé" du relais. Des plongeurs en bois tirant des fils colorés passaient au travers des trous qu'ils rencontraient. Cette opération permit une étonnante variété de motifs les plus complexes. Cette automatisation inquiéta  vivement les ouvriers tisseurs des soieries de Lyon (canuts) qui bloquèrent les métiers à l'aide de leurs sabots. Ce "sabotage" (ce mot trouve là son origine) fut le premier de l'histoire de l'industrie. Mais quand le progrès est en marche... rien ne l'arrête, en 1812 plus de 11 000 métiers à tisser Jacquard étaient en service en France et la carte perforée se répandit vite comme un moyen d'entrer de l'information dans les machines.

Son importance fut définitivement consacrée par l'inventeur américain Herman Hollerith à l'occasion du recensement de 1890. Il construisit un tabulateur électromécanique où les données étaient entrées sur cartes perforées. Cette machine permit d'obtenir rapidement des statistiques sur une population qui était passée de 2,5 millions d'individus en 1776 à plus de 60 millions en 1890. Chaque opérateur entrait entre 7000 et 8000 cartes par jour. Grâce à ce succès, la société de Hermann Hollerith fusionna avec d'autres entreprises pour constituer l'International Business Machines (IBM). Les cartes perforées ont ainsi poursuivi leur longue carrière jusque dans les années 1970.

Elles ont aujourd'hui été détrônées par deux technologies plus récentes de stockage de l'information : le magnétisme (disques durs, disquettes...) et l'optique (CD-ROM, DVD...).

II. Rappels sur la numération décimale positionnelle :

Tous les nombres entiers  même très grands s'écrivent en utilisant un alphabet de dix chiffres (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Compter jusqu'à 9 puis montrer le passage à 10. Dans ce système la valeur 10 joue un rôle particulier. On l'appelle la base du système (d'où système décimal). Le chiffre 2 par exemple n'a pas la même valeur dans 325 et dans 852. Dans le premier nombre, il vaut 10 fois plus que dans le 2ème. Sa place a donc de l'importance (d'où numération positionnelle).

Dans ce système, tout nombre est une combinaison de puissances de 10 :  325 = 3x10² + 2x10¹ + 5x10⁰

La place représente donc la puissance de 10 associée au chiffre qui l'occupe. Chaque position a un "poids" fixe 10⁰ pour le rang 0 ; 10¹ pour le rang 1 ; 10² pour le rang 2 ; 10³ pour le rang 3. On dit que c'est un code pondéré.

Exemples : 1999 = 1000 + 900 + 90 + 9 = 1x1000 + 9x100 + 9x10 + 9x1 = 1x10³ + 9x10² + 9x10¹ + 9x10⁰

FExercice : décomposer ainsi : 103 009 ; 222 669 ; 24 456 789.

III. La numération binaire :

Le système binaire naturel permet de représenter tous les nombres en utilisant uniquement les deux symboles 0 et 1 sur le même principe. Compter en utilisant le principe de numération positionnelle.

1°) Compter en binaire :

F compter en binaire jusqu’à 20.

F Vérifier en utilisant la fonction decbin d’Excel (si elle n’est pas valide, aller dans le menu outils / macros complémentaires et cocher la case « utilitaire d’analyse »)

2°) Convertir un nombre binaire en décimal :

Pour cela, il est important de connaître les puissances de 2 :

Dans le système binaire comme dans le système décimal, on peut aussi considérer tout nombre entier comme la combinaison de puissances de 2 (sachant que a⁰ = 1). 

La valeur décimale du nombre binaire 1001101 est 1x2⁶ + 1x2³ + 1x2² + 1x2⁰ soit 77.

Dans ce code, la valeur du nombre 2 présente la même importance que 10 dans le système décimal.

FConvertir en décimal : 101111 ; 11010001 ; 10011101; 11101; 111000110 et 10101010101

3°) Conversion d'un nombre décimal en binaire

Plusieurs méthodes existent :

L'une des méthode consiste à rechercher la décomposition sous la forme de puissances de 2.

Exemple : 49 = 32 + 16 + 1 = 2⁵ + 2⁴ + 2⁰ = 110001

Une autre méthode s'appuie sur le principe de la division euclidienne (jusqu'à arriver à un quotient nul) en rangeant les restes dans le sens contraire des divisions.

exemple : 19

Résultat : 10011

FExercice : écrire en binaire  les nombres 8 ; 17 ; 35 ; 47 ; 51 ;63 ; 219 ; 1000

On pourra vérifier à la machine : Avec la CASIO : se mettre en mode base puis décimal puis conversion d~o puis taper b1001101 exe ; Pour la conversion inverse: binaire puis conversion d~o puis d77exe. Ou vérifier à l’aide d’Excel.

FExercice : Concevoir une grille excel qui permet de décomposer un décimal en binaire sans utiliser la fonction decbin.

IV. Les codages binaires :

Ce système de numération a deux inconvénients :

- il entraîne de longues opérations de codage et de décodage.

- il aboutit à des écritures dont la longueur n'est pas définie par avance et par conséquent le nombre obtenu ne peut pas être traité facilement par le microprocesseur (car il ne peut traiter rapidement des mots de longueurs aléatoires).

Donc l'informatique utilise un code dérivé qui se caractérise par des combinaisons de nombres binaires à 8 chiffres  que l'on appelle bits (binary digit).

Un format de 8 bits s'appelle un octet

Les ordinateurs traitent les données par multiples de ces formats de base : ces groupements sont appelés mots.

Représentation des caractères alphanumériques :

Il ne suffit pas de savoir coder les nombres pour faire fonctionner un ordinateur.

Il faut aussi représenter l'ensemble des symboles utilisé dans le langage naturel : chiffres, lettres, caractères de ponctuation, symboles mathématiques ...

Pour pouvoir représenter les lettres de l'alphabet en majuscule et en minuscule, on utilise des codes sur au moins 7 bits.

F Combien de caractères différents un code à 7 bits permet-il de représenter ?

Le code ASCII est le plus célèbre des codes sur 8 bits. Les caractères y sont codés sur 7 bits et le 8ème est utilisé pour contrôler l'exactitude de la transmission des valeurs de différents bits lors des opérations de lecture ou d'écriture. Ce bit s'appelle alors le bit de parité, car le contrôle consiste à y mettre le symbole 0 ou 1 de telle sorte que le nombre total de 1 figurant dans la représentation soit pair. Si la valeur d'un bit est mal transmise, le nombre total de 1 change et l'ordinateur peut détecter l'erreur.

Exemples : chiffre 6 codé 00110110  (36) et la lettre A 01000001 (65)

Actuellement, on utilise des codes ASCII étendus à 8 bits. Ils offrent la possibilité de représenter les caractères semi-graphiques et les lettres accentuées

F Combien de caractères différents un code à 8 bits permet-il de représenter ?

V. Encodage d'un octet

1°) Encodage d'un octet en mémoire vive :

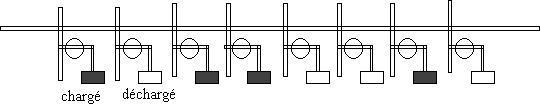
Une puce de mémoire vive est composée de transistors associés à des condensateurs. Un transistor correspond à un interrupteur et un condensateur peut emmagasiner de l'énergie .

Pour mettre en mémoire vive une information codée sur 1 octet (8 bits), le microprocesseur choisit une ligne d'adresse et envoie sur cette ligne une impulsion électrique qui ouvre les 8 transistors correspondants ; simultanément, il envoie diverse impulsions électriques qui chargent les condensateurs correspondant à des 1.

2°) Encodage sur un disque dur ou une disquette :

Pour enregistrer des 0 et des 1 sur un disque, on oriente les particules magnétiques de la surface du disque dans 2 sens différents.

Le disque dur d’un ordinateur se compose d’un ensemble de plateaux circulaires coaxiaux, recouverts d’une couche de matériau magnétique. Un champ magnétique d’orientation variable est produit par la tête de lecture / écriture. Ce champ magnétique oriente la matière magnétique du disque dur dans un sens pour inscrire un zéro et dans l’autre pour inscrire un 1 ce qui permet le stockage des informations.

Le stockage sur disquette a rigoureusement le même principe. Une disquette est un disque souple de polyester enduit d’oxyde ferrique, substance capable de conserver une aimantation. Les données sont écrites sur le disque par la tête de lecture / écriture de l’unité de disquette, qui modifie le sens de l’orientation des particules d’oxyde ferrique. L’une des orientations représente un 1 tandis que l’orientation opposée indique un 0.

3°) Encodage sur un CD :

Des capacités de stockage de plus en plus importantes sont obtenues grâce à la technologie du disque compact (CD-ROM). Ces supports sont gravés de petits trous. Entre les trous, les zones non gravées sont appelées plats. La lumière d’un faisceau laser suit la piste enregistrée. Elle est réfléchie de façon différente selon qu’elle tombe sur un trou ou sur un plat. Le lecteur traduit en 0 ou 1 les différentes réflexions.

VI. Comment transite l'information ?

Liaison parallèle : l'information transite sur 8  fils. Les 8 bits d'un octet sont envoyés en même temps.

Liaison série : l'information transite sur un seul fil. Les 8 bits d'un octet sont envoyés 1 à 1.

Le baud représente le débit d'une transmission, c'est à dire le nombre de bits transmis par secondes.

F Le Minitel est un terminal informatique qui reçoit les informations par la ligne téléphonique. Cette communication est de type série. Il travaille à la vitesse de 75 bauds. La résolution de son écran est de 25 lignes sur 40 colonnes. Chaque signe est codé sur 8 bits. Calculer le temps maximum nécessaire à la réception d'une page écran complètement remplie.

Annexe Tour de magie

Pour montrer la rapidité du tri binaire

Penser à un nombre entre 1 et 63. Parmi les 6 cartes de la page suivante, isoler celles qui le contiennent. En additionnant les 1ers nombres de ces cartes, on trouve le nombre choisi.

Jeu de cartes