Objectif : Illustrer les lois empiriques de Kepler à partir de l’étude de la trajectoire de la comète de Halley.
La Terre, tourne autour du soleil en 365 jours et 6 heures et sa trajectoire est quasi circulaire. La période de révolution n’est pas la même pour tout les corps célestes passant dans le système solaire et leur trajectoire n’est pas toujours circulaire.
Ainsi la comète de Halley revient périodiquement tous les 76 ans en se rapprochant du Soleil puis s’en éloignant en décrivant une orbite elliptique.
Edmond HALLEY (1656-1742)
Astronome et mathématicien britannique fut le premier à calculer l'orbite de la comète qui porte son nom.
Son traité le plus important « l'Astronomiae cometicae Synopsis » fut publié en 1705. Dans cette oeuvre, Halley applique les lois du mouvement de son ami Newton à toutes les données disponibles sur les comètes, et montre que les comètes aperçues en 1531, 1607 et 1682 ne sont qu'un seul et même objet céleste, qui suit une trajectoire que l'on peut calculer d'après les lois des « Principia » énoncées par Newton.
En tenant compte des perturbations de Jupiter, il annonce le retour de la comète de 1682 pour décembre 1758. Il ne s'était pas trompé de beaucoup : la comète revint, en fait, en 1759 et reçut alors le nom de comète de Halley, en l'honneur de celui qui avait compris son mouvement. Les apparitions suivantes eurent en 1835, 1910 , en 1986 et la prochaine aura lieu normalement en 2062
I ) Trajectoire de la comète de Halley :
Une comète est un corps céleste qui tourne autour du soleil, et qui fait partie du système solaire. Elle peut donc s’apparenter à une petite planète en orbite autour du Soleil.
Dans le fichier Excel,
les positions de la comète de Halley sont données par la distance r de la comète
au Soleil et la valeur de « l’anomalie vraie » av (en degré
et en radian)

La distance Soleil-Comète est donnée en unité astronomique : 1 ua = distance Terre Soleil = 1,49.1011 m
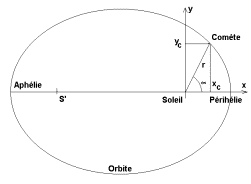
L’anomalie vraie est l’angle orienté déterminé par les vecteurs Soleil-périhélie et Soleil – Comète. Cet angle est négatif avant le passage au périhélie et positif après.
Donner l’expression des coordonnées cartésiennes x et y en fonction de r et av (exprimé en radian) Compléter le tableau et observer la trajectoire de la comète de Halley dans le référentiel héliocentrique.
A partir du document représentant cette trajectoire,
positionner l’Aphélie A , le Périhélie P, le Soleil S et le foyer S’ (symétrique
du Soleil par rapport au milieu O de AP)
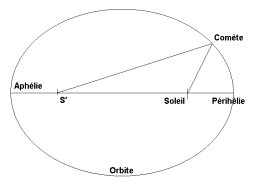
A partir de 3 ou 4 positions de la comète de Halley, vérifier que la trajectoire de la comète de Halley dans le système solaire est une ellipse dont l’un des foyers est le Soleil.
La première loi de Kepler est-elle vérifiée ?
Indiquez clairement votre démarche.
3 ) La deuxième loi de Kepler :
Dans le tableau Excel, indiquer la durée dt du déplacement entre une position repérée et sa position précédente.
Si on admet que le déplacement est presque rectiligne entre deux positions successives repérées, calculer l’aire balayées par le rayon vecteur position pendant la durée dt. Compléter le tableau.
La deuxième loi de Kepler est-elle vérifiée ? Indiquer clairement votre démarche.
Commentez ces deux affirmations et les justifier à partir des données en votre possession.
II ) La période de la comète de Halley :
La comète de Halley a une trajectoire elliptique, calcul de sa période grâce à la troisième loi de Kepler :
1 ) La troisième loi de Kepler :
Pour la Terre, que représente a, le demi-grand axe de sa trajectoire autour du soleil ?
Calculer le rapport: a3 / T2
(unités au choix.)
Calculer le demi-grand axe (a) à partir des paramètres orbitaux de la comète de Halley.
Si la troisième loi de Kepler est vérifiée, quelle serait la valeur de la période (T) de la comète de Halley. (en utilisant les mêmes unités...)
Comparer à la valeur que l’on peut déduire
de l’évolution des paramètres orbitaux donnés dans le fichier Excel.
2 ) Recherche de la masse du Soleil :
Le rapport entre le carré de la période (en s) et le cube du demi grand axe (en m3 ) de la trajectoire équivaut au rapport entre 4p2 et G (constante valant 6.67.10–11) multiplie par la masse du soleil (1.98.1030 kg ), soit :
T² = 4p ²
a3 G. Ms
Calculer la masse du Soleil et la comparer à la valeur théorique.
La composition de la comète de Halley
|
Le noyau de la comète de Halley, dont les dimensions atteignent 16x8x8 km, a l'aspect d'une grosse patate, très irrégulière et criblée de trous. L'action du Soleil entraîne une violente sublimation des glaces qui recouvrent le noyau et produit des sortes de fontaines jaillissantes formant autour de la comète une chevelure de gaz et de poussières libérées par la matrice glacée. La densité de la comète est extrêmement basse, près de 0,2 g/cm3, soit 5 fois moins élevée que celle de l'eau. Elle est composée de glaces d'eau, d'anhydride carbonique, de méthane et d'ammoniac ainsi que de poussières silicatées et de composés organiques. Ces derniers, qui sont à base de carbone, recouvrent d'une croûte la plus grande partie du noyau, faisant de la comète de Halley le corps le plus sombre du système solaire. Quand une comète se rapproche suffisamment du Soleil, l'action du vent solaire (un flux de particules chargées) a pour effet de rejeter au loin les gaz dégagés par la sublimation des glaces et les poussières de sa chevelure, formant ainsi une splendide queue, ou, plus précisément, deux queues distinctes (celle charriant les poussières est en général la plus remarquable) dont la longueur peut atteindre des dizaines, voire des centaines de millions de km. |
Photo : Vue de la comète de Halley par la
sonde Giotto |