chute

Chute d'une bille dans un fluide en régime laminaire

C'est l'évolution de la vitesse de chute qui dépend exponentiellement du temps.

L'expérience est filmée à l'aide d'une webcam, les positions de la bille sont numérisées.

Système :	bille sphérique de masse m et de volume V
Théorème fondamental:	Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système est égale au produit de sa masse par le vecteur accélération de son centre d'inertie
Référentiel :	laboratoire supposé galiléen
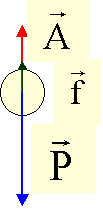
Bilan des forces :	le poids de la bille la poussée d'Archimède la force de frottement fluide	toutes ces forces sont verticales

Traduction vectorielle du théorème fondamental :

Expression algébrique (projection sur l'axe vertical orienté vers le bas) :

P - f - A = m.aG

La valeur du poids P = m.g (g = intensité de la pesanteur g = 9,81 m.s^-2)
La valeur de la poussée d'Archimède est le poids du voulme de fluide déplacé A = µ.V.g

La valeur de la force de frottement est proportionnelle à la vitesse (en régime laminaire) f = k.v

Théorème fondamental s'exprime donc par : m.g - µ.V.g- k.v = m.a_G = m.(dv/dt)

Soit par l'équation différentielle : m.(dv/dt) + k.v = m.g - µ.V.g

(la fonction du temps est la vitesse de chute v ; m.g - µ.V.g est une constante caractéristique du système)

L'équation à résoudre est du type : v' + (k/m).v = g.(1-µ.V/m) = cte

La condition initiale est v(0) = 0 (la bille est lâchée sans vitesse initiale)

La solution analytique est du type : v = v_lim[1-exp(-k/m).t]
avec v_lim = g(m-µV)/k (voir cours de maths)

Il s'agit d'une comparaison entre les résultats expérimentaux, la résolution analytique et la résolution approchée par la méthode d'Euler